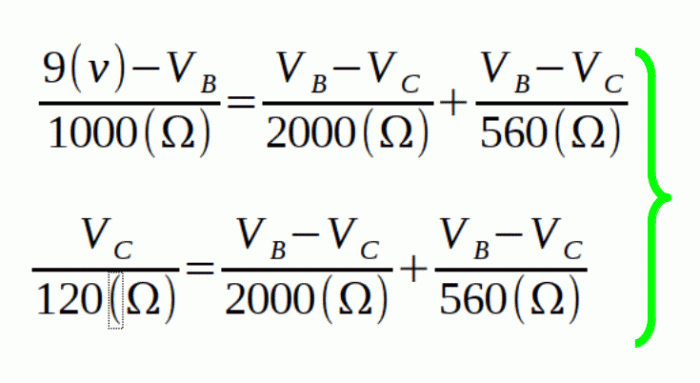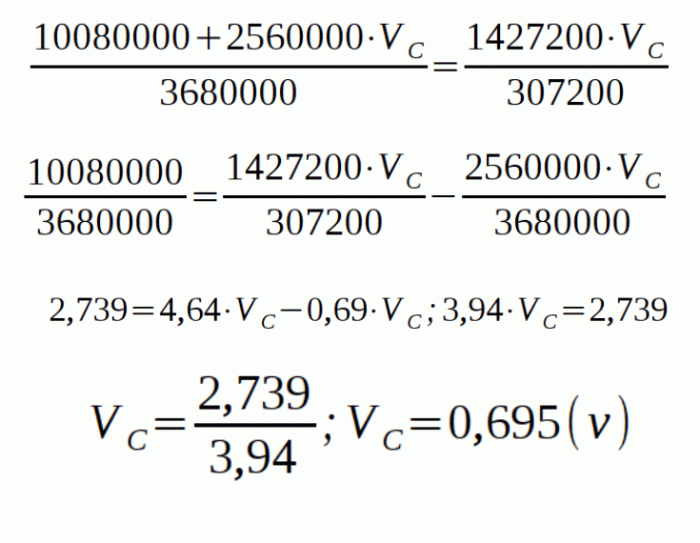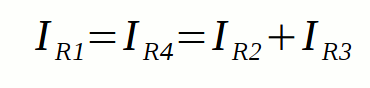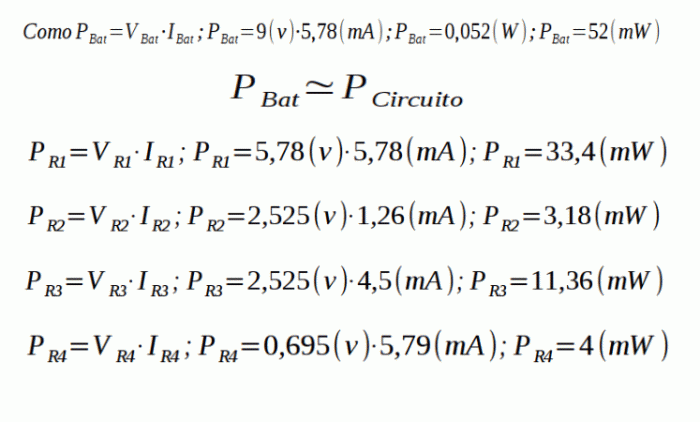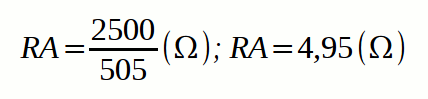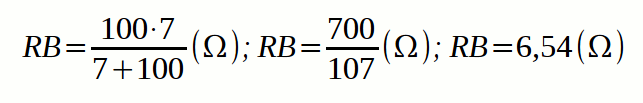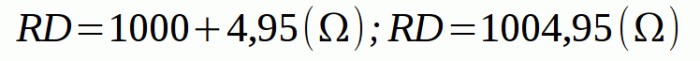Electrónica Básica: Ejercicio 2

Bienvenidos a otro artículo de nuestro curso de electrónica gratis, en esta ocasión realizaremos el ejercicio 2 para practicar las últimas lecciones del curso. A continuación, mostramos el circuito que vamos a resolver:

Figura 1. Circuito a resolver

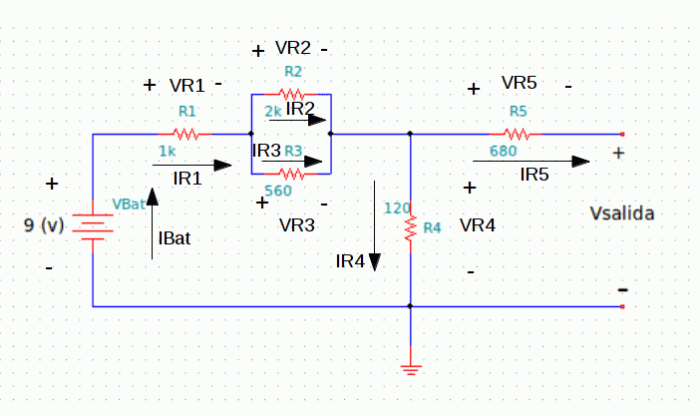
Como podemos observar en la figura 1, tenemos un circuito de 6 elementos, una batería de 9 (v) y 5 resistencias. El primer paso es dibujar las tensiones y corrientes de cada elemento en el esquema, tal y como mostramos en la figura 2, a continuación:

Figura 2. Circuito con tensiones y corrientes

Ahora que tenemos dibujadas todas las tensiones y corrientes de los elementos, vamos a dibujar los nodos del circuito mediante letras, ya que realizaremos un análisis por nodos mediante KCL, tal y como mostramos en la figura 3, a continuación:

Figura 3.Circuito anterior con nodos añadidos

Como podemos observar en la figura 3, tenemos 4 nodos, en realidad son 5 si contamos la masa, pero al ser el nodo común o de referencia, por norma no se cuenta. Si nos fijamos, hemos dibujado las polaridades a nuestro gusto, siguiendo el criterio de nuestro anterior artículo, ya os digo que son correctas, pero sino lo fueran, de todas formas al calcular detectaríamos si nuestro dibujo es incorrecto. Ahora vamos a realizar unas apreciaciones, por ejemplo podemos ver que Ibat=IR1, es decir, la batería tiene la misma corriente que la resistencia R1, esto es así porque están en serie; además también podemos ver que la tensión en la resistencia R2 es la misma que la tensión en la resistencia R3, es decir VR2=VR3, esto es así porque las dos están en paralelo. Teniendo en cuenta lo dicho, vamos a proceder a calcular el circuito, es decir debemos conocer todas las tensiones y corrientes de todos los elementos, para ello, en primer lugar, escribiremos las letras de cada nodo y a su derecha escribimos las ecuaciones del KCL, tal como mostramos en la ecuación 1, a continuación:

Ecuacion 1.KCL en los nodos

Como vemos, el nodo D no lo podemos calcular, en realidad este nodo está abierto, por lo tanto, por la resistencia R5 no circula corriente, ya que no tenemos ningún elemento después, así pues el nodo D no existe y la tensión de salida, es en realidad, la misma que en el nodo C, haciendo a la resistencia R5 superflua. Otro aspecto a tener en cuenta, es que en el nodo A, conocemos la tensión del mismo, ya que VBat=VA=9(v). Con todo esto, las ecuaciones y el circuito quedan así:

Figura 4. Circuito simplificado

Ecuacion 2. KCL en los nodos simplificados

Como podemos observar, ahora el circuito es más sencillo y ya podemos calcular. El siguiente paso, es cambiar las corrientes de cada resistencia por su cálculo correspondiente mediante la ley de ohm que vimos hace tiempo, esto es por ejemplo IR1= VR1/R1:

Ecuacion 3. Desarrollo en los nodos 1

Ahora ya hemos cambiado cada resistencia por el valor de la relación de su tensión y resistencia, mediante la ley de ohm. El siguiente paso consiste en substituir cada tensión de resistencia por la tensión de nodo, por ejemplo VR1=VA-VB, es decir, la tensión en la resistencia R1, es la diferencia de su terminal positivo (VA donde entra la corriente) y su terminal negativo (VB donde sale la corriente), tal como vimos en el artículo de polaridad. También, podemos observar, que tenemos ecuaciones extra, en realidad son de sentido común mirando el circuito. A continuación, realizamos la operación en cada nodo:

Ecuacion 4. Desarrollo KCL en los nodos 2

Ahora, como paso siguiente, vamos a substituir cada valor de tensión, solo conocemos VA y cada valor de resistencia (estas las conocemos todas):

Ecuacion 5. Desarrollo KCL en los nodos 3

Si nos fijamos bien, las ecuaciones del nodo B y C, forman un sistema de ecuaciones con 2 incógnitas, por lo tanto se puede resolver y es lo que vamos a hacer a continuación:

Ecuacion 6. Desarrollo KCL en los nodos 4

Ahora vamos a despejar VB en las dos ecuaciones (aplicando matemáticas):

Ecuacion 7. Desarrollo KCL en los nodos 5

Ahora igualamos las dos ecuaciones para hallar el valor del nodo C:

Ecuacion 8. Desarrollo KCL en los nodos 6

Ahora ya tenemos la tensión de salida como resultado y por lo tanto podemos conocer también VB:

Ecuacion 9-1. Desarrollo KCL en los nodos 7

 

Ecuacion 9-2. Continuación

Ahora ya conocemos las tensiones de cada nodo y por lo tanto también las de cada elemento. Vamos a demostrarlo:

Ecuacion 10. Desarrollo KCL en los nodos 8

Ecuacion 11. Desarrollo KCL en los nodos 9

Ahora que ya tenemos las tensiones de cada elemento, podemos calcular mediante la ley de ohm, el valor de las corrientes del circuito:

Ecuacion 12. Desarrollo KCL en los nodos 10

Como podemos observar se cumple (existe un pequeño error en los decimales):

Ecuacion 13. Desarrollo KCL en los nodos 11

Por último, solo queda calcular la potencia cedida o absorbida por cada elemento, mediante la ley de ohm. La batería cede energía y las resistencias la absorben, por lo tanto, la potencia que da la batería, la consumen las resistencias. Veamos lo con números:

Ecuacion 14. Desarrollo KCL en los nodos 12

Por lo tanto se cumple que:

Ecuacion 15. Desarrollo en los nodos 13

Lo podéis comprobar vosotros mismos. Los resultados son correctos y por lo tanto hemos terminado de calcular el ejercicio. Si tenéis dudas, realizad un comentario al respecto y os intentaremos ayudar. Ahora ya sabemos como calcular este tipo de circuitos, en el próximo artículo, trataremos la tensión alterna y como se calcula con más profundidad. Hasta pronto.

 

 

 

 

 

 

 

 

 

 

Electrónica Básica: Ejercicio I

En esta ocasión os traemos este nuevo artículo de nuestro curso de electrónica, el más elaborado hasta el momento, donde os presentamos un ejercicio de resistencias resuelto, para llevar a la práctica el estudio de resistencias en serie y paralelo.

Para esto, vamos a realizar una reducción del circuito de la Figura 1, que contiene 10 resistencias, es decir, utilizando las fórmulas de resistencia en serie y paralelo, iremos reduciendo el circuito hasta llegar a tener una sola resistencia, que será equivalente a todo el circuito.

Figura 1-Ejercicio Reducción 10 Resistencias

Para llevar a cabo la reducción, primero debemos detectar aquel conjunto de resistencias que será más fácil de reducir e ir paso a paso, en la siguiente imagen de la figura 2, os mostramos tres reducciones fáciles resaltadas en rojo, como tres conjuntos posibles que se pueden cometer en el circuito de la Figura 1:

Figura 2 Reducción A, B y C

Como podemos observar, tenemos tres conjuntos, dos resistencias en paralelo conjunto A y B, y dos resistencias en serie en el conjunto C. Así pues aplicando las fórmulas que ya publicamos en un artículo anterior, vamos a calcular la reducción de cada conjunto, como resultado obtendremos RA para el conjunto A, RB para el B y RC para el C. A continuación los cálculos:

-Cálculos conjunto A:

cálculo conjunto A, R2 y R3 en paralelo

cálculo conjunto A, R2 y R3 paralelo

-Cálculos conjunto B:

cálculos conjunto B, R6 y R7 en paralelo

cálculos conjunto B, R6 y R7 en paralelo

-Cálculos conjunto C:

cálculos conjunto C, R8, R9 y R10 en serie

Ahora que ya tenemos hechas las reducciones de los tres conjuntos, el siguiente paso es volver a dibujar el esquema con las mismas, y buscar nuevas reducciones. En la figura 3, se muestra la reducción anterior calculada y los nuevos conjuntos a reducir:

Figura 3. Reducción de conjuntos D y E

Como vemos en la figura tres, las reducciones calculadas, RA, RB y RC, hacen que podamos seguir reduciendo nuestro circuito, por lo tanto igual que antes, los nuevos conjuntos para reducir están resaltados en rojo y serán los conjuntos D y E. Como resultado obtendremos RD como dos resistencias en serie del conjunto D y RE como dos resistencias en paralelo del conjunto E. A continuación los cálculos correspondientes a esta reducción:

-Cálculos conjunto D:

cálculos conjunto D, R1 y RA en serie

cálculos conjunto D, R1 y RA en serie

-Cálculos conjunto E:

cálculos conjunto E, RB y RC en paralelo

cálculos conjunto E, RB y RC en paralelo

Ahora que ya tenemos calculadas las nuevas reducciones, vamos a volver a dibujar el esquema con las nuevas, igual que antes y también vamos a ver las siguientes reducciones a realizar, en la figura 4 a continuación:

Figura 4. Reducción conjunto F

Como podemos observar en esta figura 4, el circuito se va reduciendo a medida que vamos calculando. Ahora seguimos con el conjunto F, resaltado en rojo, que nos dará como resultado RF y tenemos que calcular dos resistencias en serie R5 y RE, a continuación:

-Cálculos conjunto F:

cálculos conjunto F, R5 y RE en serie

cálculos conjunto F, R5 y RE en serie

Una vez calculado, pasamos a dibujar el esquema con esta reducción y como anteriormente, resaltamos en rojo la nueva reducción a realizar, en la figura 5 a continuación:

Figura 5. Reducción conjunto G

Como en todos los pasos anteriores, en esta figura 5, debemos calcular la siguiente reducción del conjunto G, con dos resistencias en paralelo R4 y RF, como resultado obtendremos RG, a continuación los cálculos:

-Cálculos conjunto G:

cálculos conjunto G, R4 y RF en paralelo

cálculos conjunto G, R4 y RF en paralelo

Una vez calculado, volvemos a dibujar el circuito con esta reducción y la siguiente a calcular resaltada en rojo, en la siguiente figura 6:

Figura 6. Reducción conjunto H

Como podemos observar en esta figura 6, tenemos la última reducción del circuito, este conjunto H, dará como resultado RH, que será la resistencia total o equivalente al primer circuito con 10 resistencias, para esto nos resta calcular el conjunto H, con las resistencias RD y RG en serie, a continuación:

-Cálculos conjunto H:

cálculos conjunto H, RD y RG en serie

Así pues en la siguiente figura, obtenemos la resistencia total o equivalente y ya hemos reducido el circuito, figura 7:

Figura 7. Resultado resistencia total

Para terminar, podemos dejar mejor nuestros cálculos, ya que como vimos en un artículo anterior, todos los resultados de valores de resistencia no se fabrican, por este motivo existe el código de colores. Por lo tanto como resultado final podemos normalizar el valor de la resistencia total calculada, y será el siguiente:

-Valor final de R total:

Resultado final

Y ya está, hemos terminado nuestro ejercicio, esperamos que sea de vuestra ayuda para futuros cálculos y con este ya podréis resolver otros circuitos para encontrar la resistencia equivalente. Como extra, os dejamos en nuestra página oficial (aquí), un datasheet (hojas de características) de resistencias de carbón típicas en el mercado.

En el próximo artículo empezaremos el tema de las señales, que es la corriente continua y alterna, formas de onda, etc.

Hasta el próximo artículo.

Electrónica Básica: Ley de Ohm

Hola de nuevo,

Después de un largo período sin postear, gracias a una época de intenso trabajo, volvemos a nuestro curso de electrónica básica, ahora con la famosa ley de ohm.

Antes de que podamos analizar circuitos sobre el papel, necesitamos de herramientas de cálculo sencillas para ello, y está es la ley de ohm. El nombre lo adquirió de su creador y como pudimos fijarnos en anteriores artículos, es la unidad de medida de la resistencia, si necesitáis más info, en este link de la wikipedia encontraréis más: http://es.wikipedia.org/wiki/Ley_de_Ohm

Como podemos fijarnos en la imagen, tenemos dos triángulos con tres variables dentro, en estos se resume esta ley y es perfecto para acordarnos de una manera fácil. Vamos a describirlos:

-Triángulo izquierda:

Como vemos, en este, arriba tenemos los voltios y debajo al mismo nivel, la variable de resistencia y corriente al lado, esto significa que los voltios se dividen por una variable de debajo o multiplicamos las que están a su mismo nivel, en este caso R e I. Para entenderlo mejor vamos a ver todas las posibilidades, para hallar la variable que necesitamos, debemos taparla con un dedo en el triángulo y las otras dos será la operación que deberemos efectuar. Ejemplo de combinaciones:

-Para hallar voltaje (V), debemos tapar este con un dedo, como vemos solo nos queda R e I, como están al mismo nivel, se multiplican, así pues para hallar los voltios debemos multiplicar R por I, y tendremos los voltios resultantes.

-Para hallar Corriente (I), debemos tapar esta como antes, como vemos solo nos queda V y debajo R, como están a diferente nivel, se dividen, así pues para hallar los amperios deberemos dividir V por R, y ya está.

-Para hallar Ohms (R), debemos tapar R, y tendremos V y debajo I, por lo tanto como están a diferente nivel, se dividen, V dividido por I, y obtendremos los ohmios resultantes.

Con esto hemos acabado con el primer triángulo, con un poco de práctica lo haréis sin mirar.

-Triángulo derecha:

En este, al igual que el anterior, tenemos tres variables, solo cambia el orden y que ahora tenemos vatios en lugar de ohmios, pero el procedimiento es el mismo, si tenemos una variable a distinto nivel, se dividen, en cambio si están al mismo, se multiplican. Para entenderlo mejor veremos las combinaciones:

-Para hallar vatios (W), debemos tapar este con el dedo, como vemos solo nos queda V e I al mismo nivel, por lo tanto se multiplican y así hallaremos los vatios como resultado.

-Para hallar voltios (V), debemos tapar este, como vemos ahora solo queda W e I a distinto nivel, así pues se divide W por I, y tendremos voltios como resultado.

-Para hallar amperios (I), debemos tapar este, como podemos observar, ahora nos queda W y V a diferente nivel, como antes se divide W por V y así hallaremos los amperios.

Ahora ya sabemos calcular cualquier variable de estas cuatro en total (V, I, R y W), de forma fácil, eso si debemos llevar cuidado con los órdenes de magnitud, si, por ejemplo, tenemos kilovoltios y los dividimos por amperios, obtendremos kiloohmios y no ohmios, así pues es mejor que pasemos todo al mismo orden de magnitud para evitar errores, por ejemplo como antes, si tenemos 1 kilovoltio, debemos pasarlo a voltios para dividirlos por amperios, esto serían 1000 voltios, así si obtendremos ohmios. Si tenéis problemas, no dudéis en comentarlos, para eso están.

Hoy lo dejamos aquí, en el próximo artículo veremos unos cuantos símbolos para empezar a montar nuestros primeros circuitos de forma esquemática sobre el papel.

Hasta la próxima.